在计算机科学和数字电子领域,不同进制之间的转换是一项基本且重要的技能。无论是程序员、工程师还是计算机爱好者,掌握十六进制、十进制、八进制和二进制之间的转换方法都是必不可少的。这些进制在不同的应用场景中发挥着重要作用,例如内存地址表示(十六进制)、常规计数(十进制)、权限表示(八进制)以及底层硬件操作(二进制)。本文将深入探讨这些常用进制的转换方法,帮助读者理解其原理并熟练掌握相关技巧,从而在实际工作中更加得心应手。无论您是初学者还是有一定基础的学习者,本文都将为您提供有价值的知识和实用的指导。
4、十六进制 / 十进制 / 八进制 / 二进制 转换实例表
进制也就是进制位,常用的进制包括:二进制、八进制、十进制与十六进制,它们之间区别在于数运算时是逢几进一位。比如二进制是逢2进一位,十进制也就是我们常用的0-9是逢10进一位。
在线进制转换工具:https://www.zhanid.com/tool/hex.html
1、基本概念
数据: 在计算机中,各种信息都是以数据的形式出现的。数据经过处理后产生的结果为信息,数据是计算机中信息的载体,数据本身没有意义。
单位:位(bit)是计算机中最小的数据单位;字节(byte)是计算机中信息组织和存储的基本单位,也是计算机体系结构的基单位;1byte=8bit。
存储单位:B(字节)、KB(千字节)、MB(兆字节)、GB(吉字节)或TB(太字节)。以上是常用的换算单位,不常用的比TB更大的单位还有PB、EB、ZB、YB等。换算关系如下:
1 G = 2 10 ( 各 进 制 间 换 算 单 位 ) = 1024 M B 1G=2^{10} (各进制间换算单位)=1024 MB 1G=210(各进制间换算单位)=1024MB
1 YB = 1024 ZB 1 ZB = 1024 EB
1 EB = 1024 PB 1 PB = 1024 TB
1 TB = 1024 GB 1 GB = 1024 MB
1 MB = 1024 KB 1 KB = 1024 B(byte)
1 G = 2 10 M B = 2 20 K B = 2 30 B 1G=2^{10 }MB=2^{20}KB=2^{30} B 1G=210MB=220KB=230B
字长:计算机一次能够并行处理的二进制代码的位数。字长是衡量计算机性能的一个重要指标,字长越长,数据包含的位数越多,计算机的数据处理速度越快。计算机的字长通常是字节的整数倍,如8位、16位、32位、64位和128位等。
数制:用一组固定的符号和统一的规则来表示数值的方法。其中,按照进位方式计数的数制称为进位计数制。如二进制逢二进一,十进制逢十进一,以此类推。
数码:一个数制中表示基本数值大小的不同数字符号。十进制有10个数码(0,1,2,3,4,5,6,7,8,9)
基数:一个数值所使用数码的个数。二进制的基数为2,十进制为10。
位权:一个数值中某一位置上的数码所表示数值的大小。如:一个十进制数345,3的位权为 1 0 2 10^{2} 102,4的位权为 1 0 1 10^{1} 101, 5的位权为 1 0 0 10^{0} 100; 若是二进制数110,从右到左,0的位权则是 2 0 2^{0} 20,1的位权是 2 1 2^{1} 21,1的位权是 2 2 2^{2} 22,以此类推。
数位:指一个数中每一个数字所占的位置。如520.789,这个数,5表示百位、2表示十位、0表示个位、7表示十分位、8表示百分位、9表示千分位。
位数:一个自然数数位的个数,例如数字9,它只含一个数位,所以9就是一位数;五位数12345则含有个、十、百、干与万5个数位。
表示方式: 在计算机中,为了区分不同进制的数,可以用括号加数制基数xi下标的方式来表示不同数制的数。例如,(492)10 表示十进制数,(1001.1)2 表示二进制数,(4A9E)16表示十六进制数;也可以用带有字母的形式分别表示为(492)D、(1001.1)B和(4A9E)H。D表示十进制(Decimal),H表示十六进制(hexadecimal),B表示二进制(binary),O表示八进制(Octet)在程序设计中,为了区分不同进制数,常在数字后直接加英文学母后级来区别,如492D、1001.1B等。
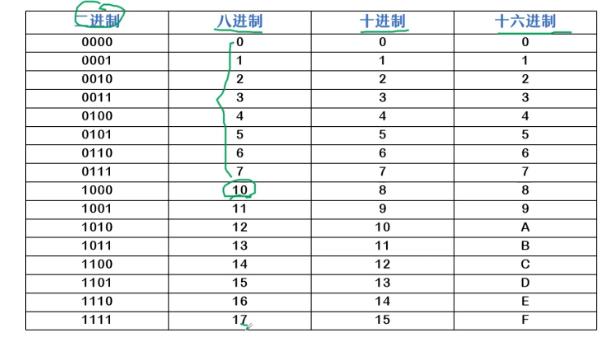
二进制:用1、0,共2位数表示
八进制:用0、1、2、3、4、5、6、7,共8位数表示
十进制:用0、1、2、3、4、5、6、7、8、9,共10位数表示
十六进制:用0、1、2、3、4、5、6、7、8、9、A=10、B=11、C=12、D=13、E=14、F=15,共16位数表示
2、计算机语言中常用的进制及表示方法
十六进制(简写为 hex 或下标 16)是一种基数为 16 的计数系统,是一种逢 16 进 1 的进位制。通常用数字 0、1、2、3、4、5、6、7、8、9 和字母 A、B、C、D、E、F(a、b、c、d、e、f)表示,其中: A~F 表示 10~15,这些称作十六进制数字。
十进制数是组成以10为基础的数字系统,有 0,1,2,3, 4, 5, 6, 7, 8, 9 十个基本数字组成。十进制,英文名称为 Decimal System,来源于希腊文 Decem,意为十。十进制计数是由印度教教徒在 1500 年前发明的,由阿拉伯人传承至 11 世纪。
八进制,Octal,缩写 OCT 或 O,一种以 8 为基数的计数法,采用 0,1,2,3,4,5,6,7 八个数字,逢八进 1。一些编程语言中常常以数字 0 开始表明该数字是八进制。八进制的数和二进制数可以按位对应(八进制一位对应二进制三位),因此常应用在计算机语言中。
二进制是计算技术中广泛采用的一种数制。 二进制数据是用 0 和 1 两个数码来表示的数。 它的基数为2,进位规则是"逢二进一",借位规则是"借一当二"。 二进制数(binaries)是逢2进位的进位制,0、1是基本算符 ;计算机运算基础采用二进制。
数制的表示有2种方法,一种表示方法是数字下标法,对于不同进制的数可以将它们加上括号再用数字下标表示进制:
例如:(110010011111)2 代表二进制数 ; (6137)8 代表八进制数
另一种是用后缀字母表示进制:
二进制 B (binary)
八进制 O (octal)
十进制 D (decimal)
十六进制 H (hexadecimal)
3、十六进制 / 十进制 / 八进制 / 二进制 转换示例
二进制(10110.01)2 转为十进制为: (22.25)10
(10110.01)2 这个二进制为5位数
则从右到左 位权依次为: 2 − 2 2^{-2} 2−2、 2 − 1 2^{-1} 2−1、 2 0 2^{0} 20、 2 1 2^{1} 21、 2 2 2^{2} 22、 2 3 2^{3} 23、 2 4 2^{4} 24
则整数部分有: 0 ∗ 2 0 + 1 ∗ 2 1 + 1 ∗ 2 2 + 0 ∗ 2 3 + 1 ∗ 2 4 0*2^{0}+1*2^{1}+1*2^{2}+0*2^{3}+1*2^{4} 0∗20+1∗21+1∗22+0∗23+1∗24 =0+2+4+0+16=22
小数部分为: 0 ∗ 2 − 1 + 1 ∗ 2 − 2 0*2^{-1}+1*2^{-2} 0∗2−1+1∗2−2=0.25
整数与小数相加为:22+0.25=22.25
八进制(232.22)8 转为十进制为:(154.28125)10
(232.22)O这个八进制为3位数
则从右到左 位权依次为:$8{-2}、$8{-1}、 8 0 、 8 1 、 8 2 8^{0}、8^{1}、8^{2} 80、81、82
则整数部分有: 2 ∗ 8 0 + 3 ∗ 8 1 + 2 ∗ 8 2 2*8^{0}+3*8^{1}+2*8^{2} 2∗80+3∗81+2∗82=2+24+128=154
小数部分为: 2 ∗ 8 − 1 + 2 ∗ 8 − 2 2*8^{-1}+2*8^{-2} 2∗8−1+2∗8−2=0.28125
整数与小数相加为:154+0.28125=154.28125
十六进制(232.6) 16转为十进制为:(562.375)10
(232)16这个十六进制为3位数
则从右到左 位权依次为: 1 6 − 1 、 1 6 0 、 1 6 1 、 1 6 2 16^{-1}、16^{0}、16^{1}、16^{2} 16−1、160、161、162
则整数部分有: 2 ∗ 1 6 0 + 3 ∗ 1 6 1 + 2 ∗ 1 6 2 2*16^{0}+3*16^{1}+2*16^{2} 2∗160+3∗161+2∗162=2+48+512=562
小数部分有: 6 ∗ 1 6 − 1 6*16^{-1} 6∗16−1=0.375
整数部分与小数部分相加:562+0.375=562.375
十进制转为其他进制数
方法:除x取余倒读法(整数),乘x取整正读法(小数)
将整数和小数分别转换,再拼接起来,也就是十进制转哪个进制就除以哪个进制的位数,即转2除以2,转8除以8,依次类推;小数位乘以该进制位数,即转8乘8,乘后去整数为,再以小数位继续乘,直至小数位为0。
十进制(225.625)10转为二进制为:(11100001.101)2
方法:除2取余倒读法(整数部分)、乘2取整正读法(小数部分)。
将该十进制数除以2,直到商为0时为止,再倒读余数1或0,得到整数部分(11100001);将该十进制的小数乘以2,取整数后,再取所的整数的小数位反复乘2,直到乘积的小数部分为0为止,即得到小数部分(101)。
十进制(1000.5)10转为八进制为:(1750.4)8
方法:除8取余倒读法(整数部分)、乘8取整正读法(小数部分)。
将该十进制数除以8,直到商为0时为止,再倒读余数1或0,得到整数部分(1750);将该十进制的小数部分乘以8,取整数后,再取所的整数的小数位反复乘8,直到乘积的小数部分为0或位数达到所需的精确度要求为止,即得到小数部分(0.4)
十进制(5621.5)10转为十六进制为:(15F5.8)16
方法:除16取余倒读法(整数部分)、乘16取整正读法(小数部分)。
将该十进制数除以16,直到商为0时为止,再倒读余数1或0,得到整数部分(15F5);将该十进制的小数部分乘以16,取整数,反复乘16,直到乘积的小数部分为0,即得到小数部分。
二进制(1101001.101)2转八进制为:(151.5)8
方法:3位分一组,按2相加
以小数点为界,整数部分从右向左每3位为一组,若最后一组不足3位,则在最高位前面添0补足3位,然后将每组中的二进制数按2的权相加,得到对应的八进制数;小数部分从左向右每3位分为一组,最后一组不足3位时,尾部用0补足3位,同上按2权相加,然后按照顺序写出每组二进制数对应的八进制数即可。
二进制(101110011000111011.1)2转十六进制为:(2E63B.8)16
方法:4位分一组,按2相加
以小数点为界,整数部分从右向左每4位为一组,若最后一组不足4位,则在最高位前面添0补足4位,然后将每组中的二进制数按权相加,得到对应的十六进制数;小数部分从左向右每4位分为一组,最后一组不足4位时,尾部用0补足4位,同上按2权相加,然后按照顺序写出每组二进制数对应的十六进制数即可。
八进制(162.4)8转二进制为:(1110101.1)2
方法:各除2取余,0补够3位
从八进制数的低位开始,将每一位上的八进制数除以2得到对应的3位二进制数,位数不够的补0;小数部分也同上进行转换。
十六进制(3B7D)16转二进制为:(11101101111101)2
方法:各除2取余,0补够4位
从十六进制数的低位开始,将每一位上的十六进制数写成对应的4位二进制数,位数不够的补0;小数部分也同上进行转换。
4、十六进制 / 十进制 / 八进制 / 二进制 转换实例表
| 十进制 Decimal | 八进制 Octal | 十六进制 Hexadecimal | 二进制 Binary |
|---|---|---|---|
| 0 | /000 | 0x00 | 0 0 0 0 0 0 0 0 |
| 1 | /001 | 0x01 | 0 0 0 0 0 0 0 1 |
| 2 | /002 | 0x02 | 0 0 0 0 0 0 1 0 |
| 3 | /003 | 0x03 | 0 0 0 0 0 0 1 1 |
| 4 | /004 | 0x04 | 0 0 0 0 0 1 0 0 |
| 5 | /005 | 0x05 | 0 0 0 0 0 1 0 1 |
| 6 | /006 | 0x06 | 0 0 0 0 0 1 1 0 |
| 7 | /007 | 0x07 | 0 0 0 0 0 1 1 1 |
| 8 | /010 | 0x08 | 0 0 0 0 1 0 0 0 |
| 9 | /011 | 0x09 | 0 0 0 0 1 0 0 1 |
| 10 | /012 | 0x0A | 0 0 0 0 1 0 1 0 |
| 11 | /013 | 0x0B | 0 0 0 0 1 0 1 1 |
| 12 | /014 | 0x0C | 0 0 0 0 1 1 0 0 |
| 13 | /015 | 0x0D | 0 0 0 0 1 1 0 1 |
| 14 | /016 | 0x0E | 0 0 0 0 1 1 1 0 |
| 15 | /017 | 0x0F | 0 0 0 0 1 1 1 1 |
| 16 | /020 | 0x10 | 0 0 0 1 0 0 0 0 |
| 17 | /021 | 0x11 | 0 0 0 1 0 0 0 1 |
| 18 | /022 | 0x12 | 0 0 0 1 0 0 1 0 |
| 19 | /023 | 0x13 | 0 0 0 1 0 0 1 1 |
| 20 | /024 | 0x14 | 0 0 0 1 0 1 0 0 |
| 21 | /025 | 0x15 | 0 0 0 1 0 1 0 1 |
| 22 | /026 | 0x16 | 0 0 0 1 0 1 1 0 |
| 23 | /027 | 0x17 | 0 0 0 1 0 1 1 1 |
| 24 | /030 | 0x18 | 0 0 0 1 1 0 0 0 |
| 25 | /031 | 0x19 | 0 0 0 1 1 0 0 1 |
| 26 | /032 | 0x1A | 0 0 0 1 1 0 1 0 |
| 27 | /033 | 0x1B | 0 0 0 1 1 0 1 1 |
| 28 | /034 | 0x1C | 0 0 0 1 1 1 0 0 |
| 29 | /035 | 0x1D | 0 0 0 1 1 1 0 1 |
| 30 | /036 | 0x1E | 0 0 0 1 1 1 1 0 |
| 31 | /037 | 0x1F | 0 0 0 1 1 1 1 1 |
| 32 | /040 | 0x20 | 0 0 1 0 0 0 0 0 |
| 33 | /041 | 0x21 | 0 0 1 0 0 0 0 1 |
| 34 | /042 | 0x22 | 0 0 1 0 0 0 1 0 |
| 35 | /043 | 0x23 | 0 0 1 0 0 0 1 1 |
| 36 | /044 | 0x24 | 0 0 1 0 0 1 0 0 |
| 37 | /045 | 0x25 | 0 0 1 0 0 1 0 1 |
| 38 | /046 | 0x26 | 0 0 1 0 0 1 1 0 |
| 39 | /047 | 0x27 | 0 0 1 0 0 1 1 1 |
| 40 | /050 | 0x28 | 0 0 0 1 1 0 0 0 |
| 41 | /051 | 0x29 | 0 0 0 1 1 0 0 1 |
| 42 | /052 | 0x2A | 0 0 1 0 1 0 1 0 |
| 43 | /053 | 0x2B | 0 0 1 0 1 0 1 1 |
| 44 | /054 | 0x2C | 0 0 1 0 1 1 0 0 |
| 45 | /055 | 0x2D | 0 0 1 0 1 1 0 1 |
| 46 | /056 | 0x2E | 0 0 1 0 1 1 1 0 |
| 47 | /057 | 0x2F | 0 0 1 0 1 1 1 1 |
| 48 | /060 | 0x30 | 0 0 1 1 0 0 0 0 |
| 49 | /061 | 0x31 | 0 0 1 1 0 0 0 1 |
| 50 | /062 | 0x32 | 0 0 1 1 0 0 1 0 |
| 51 | /063 | 0x33 | 0 0 1 1 0 0 1 1 |
| 52 | /064 | 0x34 | 0 0 1 1 0 1 0 0 |
| 53 | /065 | 0x35 | 0 0 1 1 0 1 0 1 |
| 54 | /066 | 0x36 | 0 0 1 1 0 1 1 0 |
| 55 | /067 | 0x37 | 0 0 1 1 0 1 1 1 |
| 56 | /070 | 0x38 | 0 0 1 1 1 0 0 0 |
| 57 | /071 | 0x39 | 0 0 1 1 1 0 0 1 |
| 58 | /072 | 0x3A | 0 0 1 1 1 0 1 0 |
| 59 | /073 | 0x3B | 0 0 1 1 1 0 1 1 |
| 60 | /074 | 0x3C | 0 0 1 1 1 1 0 0 |
| 61 | /075 | 0x3D | 0 0 1 1 1 1 0 1 |
| 62 | /076 | 0x3E | 0 0 1 1 1 1 1 0 |
| 63 | /077 | 0x3F | 0 0 1 1 1 1 1 1 |
| 64 | /100 | 0x40 | 0 1 0 0 0 0 0 0 |
| 65 | /101 | 0x41 | 0 1 0 0 0 0 0 1 |
| 66 | /102 | 0x42 | 0 1 0 0 0 0 1 0 |
| 67 | /103 | 0x43 | 0 1 0 0 0 0 1 1 |
| 68 | /104 | 0x44 | 0 1 0 0 0 1 0 0 |
| 69 | /105 | 0x45 | 0 1 0 0 0 1 0 1 |
| 70 | /106 | 0x46 | 0 1 0 0 0 1 1 0 |
| 71 | /107 | 0x47 | 0 1 0 0 0 1 1 1 |
| 72 | /110 | 0x48 | 0 1 0 0 1 0 0 0 |
| 73 | /111 | 0x49 | 0 1 0 0 1 0 0 1 |
| 74 | /112 | 0x4A | 0 1 0 0 1 0 1 0 |
| 75 | /113 | 0x4B | 0 1 0 0 1 0 1 1 |
| 76 | /114 | 0x4C | 0 1 0 0 1 1 0 0 |
| 77 | /115 | 0x4D | 0 1 0 0 1 1 0 1 |
| 78 | /116 | 0x4E | 0 1 0 0 1 1 1 0 |
| 79 | /117 | 0x4F | 0 1 0 0 1 1 1 1 |
| 80 | /120 | 0x50 | 0 1 0 1 0 0 0 0 |
| 81 | /121 | 0x51 | 0 1 0 1 0 0 0 1 |
| 82 | /122 | 0x52 | 0 1 0 1 0 0 1 0 |
| 83 | /123 | 0x53 | 0 1 0 1 0 0 1 1 |
| 84 | /124 | 0x54 | 0 1 0 1 0 1 0 0 |
| 85 | /125 | 0x55 | 0 1 0 1 0 1 0 1 |
| 86 | /126 | 0x56 | 0 1 0 1 0 1 1 0 |
| 87 | /127 | 0x57 | 0 1 0 1 0 1 1 1 |
| 88 | /130 | 0x58 | 0 1 0 1 1 0 0 0 |
| 89 | /131 | 0x59 | 0 1 0 1 1 0 0 1 |
| 90 | /132 | 0x5A | 0 1 0 1 1 0 1 0 |
| 91 | /133 | 0x5B | 0 1 0 1 1 0 1 1 |
| 92 | /134 | 0x5C | 0 1 0 1 1 1 0 0 |
| 93 | /135 | 0x5D | 0 1 0 1 1 1 0 1 |
| 94 | /136 | 0x5E | 0 1 0 1 1 1 1 0 |
| 95 | /137 | 0x5F | 0 1 0 1 1111 |
| 96 | /140 | 0x60 | 0 1 1 0 0 0 0 0 |
| 97 | /141 | 0x61 | 0 1 1 0 0 0 0 1 |
| 98 | /142 | 0x62 | 0 1 1 0 0 0 1 0 |
| 99 | /143 | 0x63 | 0 1 1 0 0 0 1 1 |
| 100 | /144 | 0x64 | 0 1 1 0 0 1 0 0 |
| 101 | /145 | 0x65 | 0 1 1 0 0 1 0 1 |
| 102 | /146 | 0x66 | 0 1 1 0 0 1 1 0 |
| 103 | /147 | 0x67 | 0 1 1 0 0 1 1 1 |
| 104 | /150 | 0x68 | 0 1 1 0 1 0 0 0 |
| 105 | /151 | 0x69 | 0 1 1 0 1 0 0 1 |
| 106 | /152 | 0x6A | 0 1 1 0 1 0 1 0 |
| 107 | /153 | 0x6B | 0 1 1 0 1 0 1 1 |
| 108 | /154 | 0x6C | 0 1 1 0 1 1 0 0 |
| 109 | /155 | 0x6D | 0 1 1 0 1 1 0 1 |
| 110 | /156 | 0x6E | 0 1 1 0 1 1 1 0 |
| 111 | /157 | 0x6F | 0 1 1 0 1 1 1 1 |
| 112 | /160 | 0x70 | 0 1 1 1 0 0 0 0 |
| 113 | /161 | 0x71 | 0 1 1 1 0 0 0 1 |
| 114 | /162 | 0x72 | 0 1 1 1 0 0 1 0 |
| 115 | /163 | 0x73 | 0 1 1 1 0 0 1 1 |
| 116 | /164 | 0x74 | 0 1 1 1 0 1 0 0 |
| 117 | /165 | 0x75 | 0 1 1 1 0 1 0 1 |
| 118 | /166 | 0x76 | 0 1 1 1 0 1 1 0 |
| 119 | /167 | 0x77 | 0 1 1 1 0 1 1 1 |
| 120 | /170 | 0x78 | 0 1 1 1 1 0 0 0 |
| 121 | /171 | 0x79 | 0 1 1 1 1 0 0 1 |
| 122 | /172 | 0x7A | 0 1 1 1 1 0 1 0 |
| 123 | /173 | 0x7B | 0 1 1 1 1 0 1 1 |
| 124 | /174 | 0x7C | 0 1 1 1 1 1 0 0 |
| 125 | /175 | 0x7D | 0 1 1 1 1 1 0 1 |
| 126 | /176 | 0x7E | 0 1 1 1 1 1 1 0 |
| 127 | /177 | 0x7F | 0 1 1 1 1 1 1 1 |
| 128 | /200 | 0x80 | 1 0 0 0 0 0 0 0 |
| 129 | /201 | 0x81 | 1 0 0 0 0 0 0 1 |
| 130 | /202 | 0x82 | 1 0 0 0 0 0 1 0 |
| 131 | /203 | 0x83 | 1 0 0 0 0 0 1 1 |
| 132 | /204 | 0x84 | 1 0 0 0 0 1 0 0 |
| 133 | /205 | 0x85 | 1 0 0 0 0 1 0 1 |
| 134 | /206 | 0x86 | 1 0 0 0 0 1 1 0 |
| 135 | /207 | 0x87 | 1 0 0 0 0 1 1 1 |
| 136 | /210 | 0x88 | 1 0 0 0 1 0 0 0 |
| 137 | /211 | 0x89 | 1 0 0 0 1 0 0 1 |
| 138 | /212 | 0x8A | 1 0 0 0 1 0 1 0 |
| 139 | /213 | 0x8B | 1 0 0 0 1 0 1 1 |
| 140 | /214 | 0x8C | 1 0 0 0 1 1 0 0 |
| 141 | /215 | 0x8D | 1 0 0 0 1 1 0 1 |
| 142 | /216 | 0x8E | 1 0 0 0 1 1 1 0 |
| 143 | /217 | 0x8F | 1 0 0 0 1 1 1 1 |
| 144 | /220 | 0x90 | 1 0 0 1 0 0 0 0 |
| 145 | /221 | 0x91 | 1 0 0 1 0 0 0 1 |
| 146 | /222 | 0x92 | 1 0 0 1 0 0 1 0 |
| 147 | /223 | 0x93 | 1 0 0 1 0 0 1 1 |
| 148 | /224 | 0x94 | 1 0 0 1 0 1 0 0 |
| 149 | /225 | 0x95 | 1 0 0 1 0 1 0 1 |
| 150 | /226 | 0x96 | 1 0 0 1 0 1 1 0 |
| 151 | /227 | 0x97 | 1 0 0 1 0 1 1 1 |
| 152 | /230 | 0x98 | 1 0 0 1 1 0 0 0 |
| 153 | /231 | 0x99 | 1 0 0 1 1 0 0 1 |
| 154 | /232 | 0x9A | 1 0 0 1 1 0 1 0 |
| 155 | /233 | 0x9B | 1 0 0 1 1 0 1 1 |
| 156 | /234 | 0x9C | 1 0 0 1 1 1 0 0 |
| 157 | /235 | 0x9D | 1 0 0 1 1 1 0 1 |
| 158 | /236 | 0x9E | 1 0 0 1 1 1 1 0 |
| 159 | /237 | 0x9F | 1 0 0 1 1 1 1 1 |
| 160 | /240 | 0xA0 | 1 0 1 0 0 0 0 0 |
| 161 | /241 | 0xA1 | 1 0 1 0 0 0 0 1 |
| 162 | /242 | 0xA2 | 1 0 1 0 0 0 1 0 |
| 163 | /243 | 0xA3 | 1 0 1 0 0 0 1 1 |
| 164 | /244 | 0xA4 | 1 0 1 0 0 1 0 0 |
| 165 | /245 | 0xA5 | 1 0 1 0 0 1 0 1 |
| 166 | /246 | 0xA6 | 1 0 1 0 0 1 1 0 |
| 167 | /247 | 0xA7 | 1 0 1 0 0 1 1 1 |
| 168 | /250 | 0xA8 | 1 0 1 0 1 0 0 0 |
| 169 | /251 | 0xA9 | 1 0 1 0 1 0 0 1 |
| 170 | /252 | 0xAA | 1 0 1 0 1 0 1 0 |
| 171 | /253 | 0xAB | 1 0 1 0 1 0 1 1 |
| 172 | /254 | 0xAC | 1 0 1 0 1 1 0 0 |
| 173 | /255 | 0xAD | 1 0 1 0 1 1 0 1 |
| 174 | /256 | 0xAE | 1 0 1 0 1 1 1 0 |
| 175 | /257 | 0xAF | 1 0 1 0 1 1 1 1 |
| 176 | /260 | 0xB0 | 1 0 1 1 0 0 0 0 |
| 177 | /261 | 0xB1 | 1 0 1 1 0 0 0 1 |
| 178 | /262 | 0xB2 | 1 0 1 1 0 0 1 0 |
| 179 | /263 | 0xB3 | 1 0 1 1 0 0 1 1 |
| 180 | /264 | 0xB4 | 1 0 1 1 0 1 0 0 |
| 181 | /265 | 0xB5 | 1 0 1 1 0 1 0 1 |
| 182 | /266 | 0xB6 | 1 0 1 1 0 1 1 0 |
| 183 | /267 | 0xB7 | 1 0 1 1 0 1 1 1 |
| 184 | /270 | 0xB8 | 1 0 1 1 1 0 0 0 |
| 185 | /271 | 0xB9 | 1 0 1 1 1 0 0 1 |
| 186 | /272 | 0xBA | 1 0 1 1 1 0 1 0 |
| 187 | /273 | 0xBB | 1 0 1 1 1 0 1 1 |
| 188 | /274 | 0xBC | 1 0 1 1 1 1 0 0 |
| 189 | /275 | 0xBD | 1 0 1 1 1 1 0 1 |
| 190 | /276 | 0xBE | 1 0 1 1 1 1 1 0 |
| 191 | /277 | 0xBF | 1 0 1 1 1 1 1 1 |
| 192 | /300 | 0xC0 | 1 1 0 0 0 0 0 0 |
| 193 | /301 | 0xC1 | 1 1 0 0 0 0 0 1 |
| 194 | /302 | 0xC2 | 1 1 0 0 0 0 1 0 |
| 195 | /303 | 0xC3 | 1 1 0 0 0 0 1 1 |
| 196 | /304 | 0xC4 | 1 1 0 0 0 1 0 0 |
| 197 | /305 | 0xC5 | 1 1 0 0 0 1 0 1 |
| 198 | /306 | 0xC6 | 1 1 0 0 0 1 1 0 |
| 199 | /307 | 0xC7 | 1 1 0 0 0 1 1 1 |
| 200 | /310 | 0xC8 | 1 1 0 0 1 0 0 0 |
| 201 | /311 | 0xC9 | 1 1 0 0 1 0 0 1 |
| 202 | /312 | 0xCA | 1 1 0 0 1 0 1 0 |
| 203 | /313 | 0xCB | 1 1 0 0 1 0 1 1 |
| 204 | /314 | 0xCC | 1 1 0 0 1 1 0 0 |
| 205 | /315 | 0xCD | 1 1 0 0 1 1 0 1 |
| 206 | /316 | 0xCE | 1 1 0 0 1 1 1 0 |
| 207 | /317 | 0xCF | 1 1 0 0 1 1 1 1 |
| 208 | /320 | 0xD0 | 1 1 0 1 0 0 0 0 |
| 209 | /321 | 0xD1 | 1 1 0 1 0 0 0 1 |
| 210 | /322 | 0xD2 | 1 1 0 1 0 0 1 0 |
| 211 | /323 | 0xD3 | 1 1 0 1 0 0 1 1 |
| 212 | /324 | 0xD4 | 1 1 0 1 0 1 0 0 |
| 213 | /325 | 0xD5 | 1 1 0 1 0 1 0 1 |
| 214 | /326 | 0xD6 | 1 1 0 1 0 1 1 0 |
| 215 | /327 | 0xD7 | 1 1 0 1 0 1 1 1 |
| 216 | /330 | 0xD8 | 1 1 0 1 1 0 0 0 |
| 217 | /331 | 0xD9 | 1 1 0 1 1 0 0 1 |
| 218 | /332 | 0xDA | 1 1 0 1 1 0 1 0 |
| 219 | /333 | 0xDB | 1 1 0 1 1 0 1 1 |
| 220 | /334 | 0xDC | 1 1 0 1 1 1 0 0 |
| 221 | /335 | 0xDD | 1 1 0 1 1 1 0 1 |
| 222 | /336 | 0xDE | 1 1 0 1 1 1 1 0 |
| 223 | /337 | 0xDF | 1 1 0 1 1 1 1 1 |
| 224 | /340 | 0xE0 | 1 1 1 0 0 0 0 0 |
| 225 | /341 | 0xE1 | 1 1 1 0 0 0 0 1 |
| 226 | /342 | 0xE2 | 1 1 1 0 0 0 1 0 |
| 227 | /343 | 0xE3 | 1 1 1 0 0 0 1 1 |
| 228 | /344 | 0xE4 | 1 1 1 0 0 1 0 0 |
| 229 | /345 | 0xE5 | 1 1 1 0 0 1 0 1 |
| 230 | /346 | 0xE6 | 1 1 1 0 0 1 1 0 |
| 231 | /347 | 0xE7 | 1 1 1 0 0 1 1 1 |
| 232 | /350 | 0xE8 | 1 1 1 0 1 0 0 0 |
| 233 | /351 | 0xE9 | 1 1 1 0 1 0 0 1 |
| 234 | /352 | 0xEA | 1 1 1 0 1 0 1 0 |
| 235 | /353 | 0xEB | 1 1 1 0 1 0 1 1 |
| 236 | /354 | 0xEC | 1 1 1 0 1 1 0 0 |
| 237 | /355 | 0xED | 1 1 1 0 1 1 0 1 |
| 238 | /356 | 0xEE | 1 1 1 0 1 1 1 0 |
| 239 | /357 | 0xEF | 1 1 1 0 1 1 1 1 |
| 240 | /360 | 0xF0 | 1 1 1 1 0 0 0 0 |
| 241 | /361 | 0xF1 | 1 1 1 1 0 0 0 1 |
| 242 | /362 | 0xF2 | 1 1 1 1 0 0 1 0 |
| 243 | /363 | 0xF3 | 1 1 1 1 0 0 1 1 |
| 244 | /364 | 0xF4 | 1 1 1 1 0 1 0 0 |
| 245 | /365 | 0xF5 | 1 1 1 1 0 1 0 1 |
| 246 | /366 | 0xF6 | 1 1 1 1 0 1 1 0 |
| 247 | /367 | 0xF7 | 1 1 1 1 0 1 1 1 |
| 248 | /370 | 0xF8 | 1 1 1 1 1 0 0 0 |
| 249 | /371 | 0xF9 | 1 1 1 1 1 0 0 1 |
| 250 | /372 | 0xFA | 1 1 1 1 1 0 1 0 |
| 251 | /373 | 0xFB | 1 1 1 1 1 0 1 1 |
| 252 | /374 | 0xFC | 1 1 1 1 1 1 0 0 |
| 253 | /375 | 0xFD | 1 1 1 1 1 1 0 1 |
| 254 | /376 | 0xFE | 1 1 1 1 1 1 1 0 |
| 255 | /377 | 0xFF | 1 1 1 1 1 1 1 1 |
总结
通过本文的详细讲解,我们了解了十六进制、十进制、八进制和二进制之间的转换方法及其应用场景。掌握了这些转换技巧后,您将能够在计算机编程、数据分析、硬件设计等领域中更加自如地操作和处理数值信息。希望本文的内容对您有所帮助,并能为您的学习和工作带来便利。如果您有任何疑问或需要进一步的指导,请随时留言,我们将竭诚为您解答。感谢您的阅读,期待您的进步与成长!
本文由@zhanid 原创发布。
该文章观点仅代表作者本人,不代表本站立场。本站不承担相关法律责任。
如若转载,请注明出处:https://www.zhanid.com/dnzs/2327.html




















