圆的周长怎么算？圆的周长计算公式及方法详解

圆是一种常见的几何图形，在日常生活和科学研究中有广泛应用。圆的周长，即围成圆的曲线的长度，是圆的重要属性之一。本文ZHANID工具网将详细讲解如何计算圆的周长，并给出具体的计算公式和方法。

一、圆的基本概念

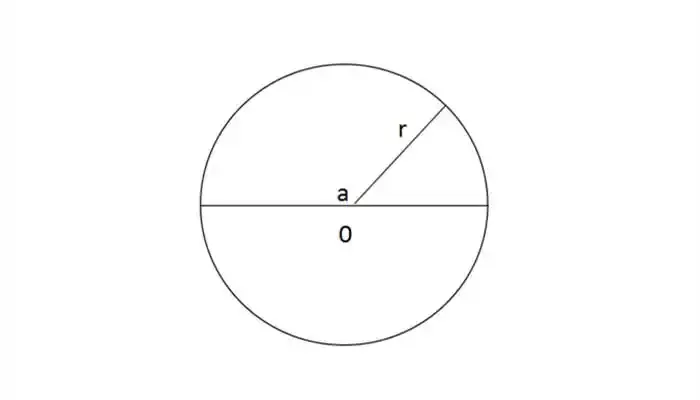
圆是一种几何图形，指的是平面中到一个定点距离为定值的所有点的集合。这个给定的点称为圆的圆心，作为定值的距离称为圆的半径。圆的直径是通过圆心并且两个端点都在圆周上的线段，半径是直径的一半。

圆的周长是指围成圆的曲线的长度，用字母C表示。为了计算圆的周长，我们需要引入一个特殊的常数——圆周率π。圆周率π是一个无理数，其值约为3.1415926……，它在圆的周长和面积计算中起着关键作用。

二、圆的周长计算公式

圆的周长计算公式主要有两种形式：

公式一：C = πd

• 其中，d是圆的直径。这个公式表示，圆的周长等于圆周率π乘以圆的直径。

公式二：C = 2πr

• 其中，r是圆的半径。这个公式表示，圆的周长等于圆周率π乘以半径的2倍。

这两个公式是等价的，因为圆的直径d等于半径r的2倍，即d = 2r。因此，将d = 2r代入公式一，即可得到公式二。

三、计算圆周长的方法

根据圆的周长计算公式，我们可以采用以下两种方法计算圆的周长：

方法一：使用直径计算

如果已知圆的直径d，我们可以直接利用公式C = πd计算圆的周长。例如，某个圆的直径是4厘米，那么它的周长就是C = π × 4 = 12.566370614359172厘米(取π的近似值3.1415926……)。

方法二：使用半径计算

如果已知圆的半径r，我们可以利用公式C = 2πr计算圆的周长。例如，某个圆的半径是2厘米，那么它的周长就是C = 2π × 2 = 12.566370614359172厘米(取π的近似值3.1415926……)。

四、圆周率的计算与精度

圆周率π是一个无理数，其值无法精确表示为一个有限小数或分数。在实际应用中，我们通常使用π的近似值进行计算。历史上，人们通过多种方法计算了π的近似值，包括几何方法、代数方法、数值方法等。

随着计算机技术的发展，我们可以使用高精度算法计算π的值。目前，人们已经计算出了π的上亿位小数。然而，在大多数情况下，我们只需要使用π的几位或几十位小数进行计算，就可以得到足够精确的结果。

五、圆的周长与实际应用

圆的周长在日常生活和科学研究中有着广泛的应用。以下是一些常见的应用场景：

轮胎周长

汽车、自行车等交通工具的轮胎都是圆形的。为了计算轮胎的周长，我们需要知道轮胎的直径或半径，然后利用圆的周长计算公式进行计算。轮胎的周长对于计算车辆的行驶距离、速度等参数具有重要意义。

圆形管道

在一些工程应用中，管道的形状是圆形的。为了计算圆形管道的周长，我们需要知道管道的直径，然后利用圆的周长计算公式进行计算。圆形管道的周长对于计算管道的流量、压力等参数具有重要意义。

圆形零件

在机械制造中，经常需要加工圆形零件。为了计算圆形零件的周长，我们需要知道零件的直径或半径，然后利用圆的周长计算公式进行计算。圆形零件的周长对于计算零件的尺寸、加工精度等参数具有重要意义。

圆形场地

在体育场馆、游乐园等场所，经常需要布置圆形场地。为了计算圆形场地的周长，我们需要知道场地的直径或半径，然后利用圆的周长计算公式进行计算。圆形场地的周长对于计算场地的面积、容纳人数等参数具有重要意义。

六、圆的周长与面积的关系

除了周长，圆的面积也是圆的重要属性之一。圆的面积计算公式为S = πr²，其中r是圆的半径。圆的面积表示圆所占平面的大小。

圆的周长和面积之间存在一定的关系。当圆的半径增大时，圆的周长和面积都会增大。然而，周长和面积的增长速度是不同的。具体来说，当半径增大一倍时，圆的周长会增大一倍，但圆的面积会增大四倍。这是因为圆的周长与半径成正比，而圆的面积与半径的平方成正比。

七、圆的周长与几何图形的比较

除了圆，还有其他一些常见的几何图形，如正方形、长方形、三角形等。这些几何图形的周长也有各自的计算公式。

正方形的周长

正方形的周长计算公式为C = 4a，其中a是正方形的边长。正方形的周长表示正方形四条边的长度之和。

长方形的周长

长方形的周长计算公式为C = 2(l + w)，其中l是长方形的长度，w是长方形的宽度。长方形的周长表示长方形四条边的长度之和。

三角形的周长

三角形的周长计算公式为C = a + b + c，其中a、b、c分别是三角形的三条边长。三角形的周长表示三角形三条边的长度之和。

与这些几何图形相比，圆的周长具有一些特殊性质。例如，圆的周长是连续的曲线，而其他几何图形的周长是由直线段组成的。此外，圆的周长与半径成正比，而其他几何图形的周长与边长之间的关系可能更加复杂。

八、圆的周长与数学定理

圆的周长与一些数学定理密切相关。以下是一些常见的数学定理：

圆周角定理

圆周角定理指出，在同圆或等圆中，同弧或等弧所对的圆周角相等。这个定理在圆的周长计算中具有一定的应用价值。

垂径定理

垂径定理指出，垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。这个定理在圆的周长计算中也有一定的应用。

圆的切线性质

圆的切线性质指出，圆的切线垂直于过切点的半径。这个性质在圆的周长计算中有时可以简化计算过程。

九、圆的周长与几何作图

在几何作图中，我们经常需要绘制圆形图形。为了绘制精确的圆形图形，我们需要知道圆的周长或直径等参数。以下是一些常见的几何作图方法：

使用圆规绘制圆形

圆规是一种常用的几何作图工具，可以用来绘制圆形图形。在使用圆规绘制圆形时，我们需要先确定圆的半径或直径，然后将圆规的两脚张开相应的距离，在纸面上旋转一周即可绘制出圆形图形。

使用刻度尺和圆规绘制圆形

有时我们需要绘制具有特定周长的圆形图形。这时，我们可以使用刻度尺和圆规相结合的方法进行绘制。首先，我们使用刻度尺测量出所需的周长长度，然后利用圆规的张开距离与周长之间的关系计算出圆的半径或直径，最后在纸面上绘制出圆形图形。

十、相关工具

• 圆形计算器：https://www.zhanid.com/tool/circle-calculator.html

结论

圆的周长是圆的重要属性之一，具有广泛的应用价值。本文详细介绍了圆的周长计算公式、计算方法以及与其他几何图形和数学定理的关系。通过本文的学习，我们可以更好地理解和应用圆的周长知识，为日常生活和科学研究提供有力的支持。

在未来的研究中，我们可以进一步探讨圆的周长与其他几何属性之间的关系，以及如何利用现代计算技术和算法提高圆周率的计算精度和效率。此外，我们还可以将圆的周长知识应用于更广泛的领域，如物理学、工程学、计算机科学等，为推动科学技术的发展做出更大的贡献。