排列组合中的C和A怎么算（附计算公式和方法）

排列组合是组合数学中最基本的概念之一，在许多领域中都有广泛的应用。排列和组合分别指的是从给定数量的元素中取出指定数量的元素进行排序和不考虑排序的组合。本文ZHANID将详细介绍排列组合中的C(组合)和A(排列)的计算方法，并附上具体的计算公式和实例。

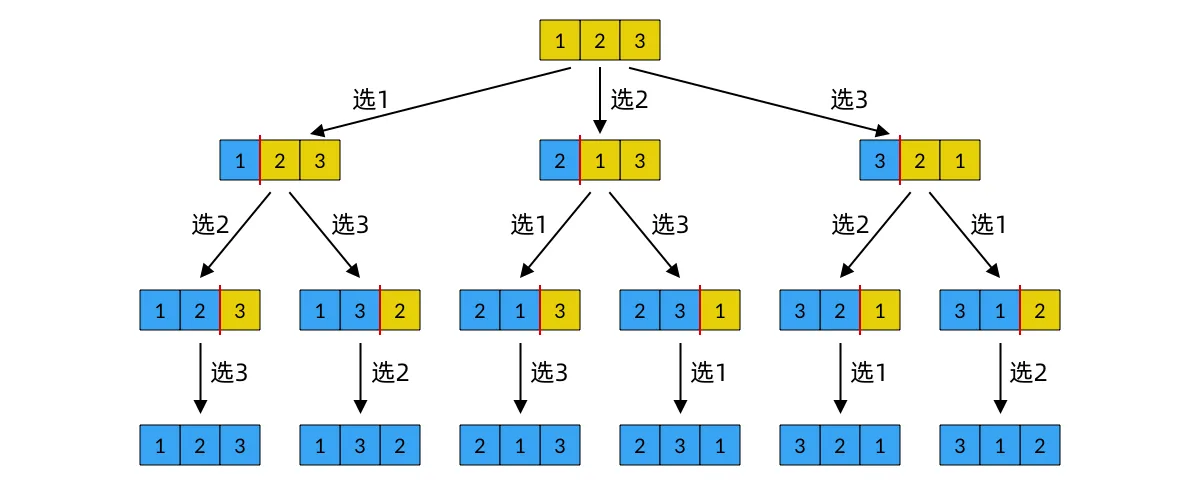
一、排列(A)的计算

排列指的是从n个不同的元素中，任意取出m个不同元素(m≤n)，按照一定的顺序排成一列，称为n个不同元素中取出m个元素的一个排列。排列数的计算公式如下：

其中，n!表示n的阶乘，即n × (n-1) × (n-2) × ... × 1。

举个例子，假设我们有4个元素{A, B, C, D}，从中取出2个元素进行排列，那么排列数A(4,2)的计算过程如下：

A(4,2) = 4 × 3 = 12

因此，从4个元素中取出2个元素进行排列，共有12种不同的排列方式。

二、组合(C)的计算

组合指的是从n个不同的元素中，任意取出m个不同元素(m≤n)，不考虑取出元素的顺序，所组成的一个组合。组合数的计算公式如下：

其中，P(n,m)表示排列数，P(m,m)表示m个元素的全排列数。

举个例子，假设我们有5个元素{A, B, C, D, E}，从中取出3个元素进行组合，那么组合数C(5,3)的计算过程如下：

C(5,3) = 5! / [3! × (5-3)!] = 120 / (6 × 2) = 10

因此，从5个元素中取出3个元素进行组合，共有10种不同的组合方式。

三、排列组合的基本概念

排列组合是组合数学中最基本的概念之一。排列指的是从给定数量的元素中取出指定数量的元素进行排序，而组合则是指从给定数量的元素中取出指定数量的元素，不考虑排序。

• 排列的定义：从n个不同元素中，任意取出m个不同元素(m≤n)，按照一定的顺序排成一列，称为n个不同元素中取出m个元素的一个排列。

• 组合的定义：从n个不同元素中，任意取出m个不同元素(m≤n)，不考虑取出元素的顺序，所组成的一个组合。

四、排列组合的计算方法

排列组合的计算方法主要有两种：一种是直接计算排列数和组合数，另一种是通过排列组合的性质进行计算。

直接计算排列数和组合数

直接计算排列数和组合数的方法是通过排列组合的定义进行计算。具体步骤如下：

(1)排列数的计算：从n个不同元素中取出m个不同元素，按照一定的顺序排成一列，称为n个不同元素中取出m个元素的一个排列。排列数的计算公式为：

(2)组合数的计算：从n个不同元素中，任意取出m个不同元素(m≤n)，不考虑取出元素的顺序，所组成的一个组合。组合数的计算公式为：

通过排列组合的性质进行计算

排列组合有许多重要的性质，这些性质可以帮助我们更方便地计算排列数和组合数。下面列举了一些常用的排列组合性质：

• (1)排列数的性质：A(n,m) = n × A(n-1,m-1)

• (2)组合数的性质：C(n,m) = C(n-1,m-1) + C(n-1,m)

• (3)二项式定理：(a+b)^n = Σ(k=0 to n) C(n,k) × a^(n-k) × b^k

五、排列组合的应用

排列组合在许多领域中都有广泛的应用，例如计算机科学、统计学、物理学、化学等。在计算机科学中，排列组合常用于算法设计和数据分析;在统计学中，排列组合常用于概率计算和抽样调查;在物理学和化学中，排列组合常用于分子结构分析和化学反应计算。

六、总结

排列组合是组合数学中最基本的概念之一，它在许多领域中都有广泛的应用。排列指的是从给定数量的元素中取出指定数量的元素进行排序，而组合则是指从给定数量的元素中取出指定数量的元素，不考虑排序。排列数和组合数的计算方法主要有两种：一种是直接计算排列数和组合数，另一种是通过排列组合的性质进行计算。通过学习排列组合的基本概念和计算方法，我们可以更好地理解和应用排列组合的知识。